https://www.youtube.com/watch?v=nHt7BHyJGko
https://www.youtube.com/watch?v=lIKSQgy7M2s
https://www.youtube.com/watch?v=ZMgax46Rd3g
뉴런

우리가 인공 지능에게 바라는 것은 추론 하기 입니다.
| Input | Output |
| 집이 얼마나 큰가? | 가격을 추론한다 |
| 얼마나 공부를 많이 했는가? | 시험 점수를 추론한다 |

학창시절 생물이나 과학시간에 신경망을 이루는 뉴런에 대해서 배운 기억이 있을 것입니다. 신경망의 많은 수의 뉴런 그러니까 신경 세포들이 연결되어 만들어 진다.
우리 두뇌속에는 대략 1000억개의 뉴런들이 복잡하게 연결되어 있습니다.
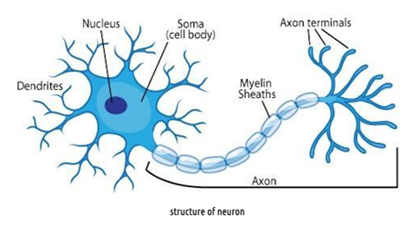
뉴런이 하는 일은 수상돌기(덴드라이트)를 통해 여러 개의 이웃 뉴런들로 부터 전기 신호를 입력받고 축삭 돌기 말단(엑손 터미널)을 통해 다른 뉴런에게 전기 신호를 내보내는 것입니다.
이 때 다른 뉴런들로부터 입력받은 신호를 어떻게 처리하여 어떤 신호를 내보낼지는 각 뉴런들의 속성에 따라 다릅니다.
복잡하게 연결된 수많은 뉴런들은 오랜 경험을 통해 각기 다른 속성을 갖도록 훈련되어 왔고 어떤 입력을 받았는지에 '따라 다양한 정보를 전달하고 출력해내기 때문에 우리가 여러가지 방법으로 행동할 수 있는 것입니다.
인공 뉴런
하나의 뉴런
다음은 하나의 인공 뉴런입니다.

이 뉴런의 역할은 입력x가 들어 오면 출력y를 내보내는 것입니다. 이때 추가로 들어가는 바이어스b도 있다는 점을 눈여겨 봅시다.
바이어스b는 외부에서 입력해주는 것이 아니라 뉴럴 네트워크 자체 속성이기 때문에 훈련에 따라 그 값이 결정된다는 점이 그 차이입니다.
여러 뉴런

이 그림에서 볼 수 있듯이 한 뉴런의 입력과 출력은 하나일 수도 있고 여러 개일 수도 있습니다. 각 뉴런의 입력은 외부에서 들어오는 값일 수도 있고 다른 뉴런에서 출력한 값을 입력으로 받아 들일 수도 있습니다. 마찬가지로 모든 뉴런은 출력 값을 다른 뉴런으로 전달할 수도있고 외부로 출력 할 수도 있습니다.
이렇게 많은 수의 뉴런들이 다양한 방식으로 연결되어 복잡한 기능을 수행할 수 있도록 만든 것이 바로 인공 뉴럴 네트워크 즉 인공 신경망입니다.
인공 뉴런 내부
인공 뉴런 안에서는 어떤 일이 벌어지는지 살펴봅시다.

외부에서 들어온 입력값(x)이 얼마나 중요한 지를 결정하기 위한 가중치 웨이트(w)와 곱합니다. 그리고 거기에 바이어스를 더해서 썸 시그마(σ) 값을 결정합니다.
σ = w⋅x + b
이런 단순한 형태가 됩니다.

예를 들어 살펴봅시다. 이 경우 시그마 값이 2가 됩니다.
Affine Sum(아파인 혹은 아핀 썸)

이렇게 가중치 그 다음에 바이어스를 고려해서 합을 구하는 것을 Affine sum이라고 부릅니다. 행렬의 곱 형태로 바꿔 보면 Affine sum의 의미가 좀 더 분명하게 드러납니다.
활성화 함수(Activation Functions)

활성화는 어떤 함수 f를 통해서 이루어집니다. 당연히 함수 f가 어떤 형태인지가 중요하겠죠.

인공지능 분야에서는 이 액티베이션 펑션을 다양한 형태로 사용합니다. 가장 많이 사용되는 것이 ReLU(Rectified Liner Unit)입니다. 예전에 굉장히 자주 사용되던 시그모이드 함수가 있습니다.
Affine sum으로 얻어진 시그마를 함수f를 통해서 액티베이션을 시키고 이 값은 출력 y 값이 됩니다. 이 y 값은 사용자가 바로 받아가거나 다른 뉴런의 입력값으로 사용되기도 합니다.
Feed-forward

이렇게 입력 x를 넣고 출력 y를 받아내는 것을 feed forward라고 합니다.
identity 함수를 사용하는 경우입니다. f(x) = x

입력한 값 그대로 이므로 w⋅x + b가 출력됩니다.
다양한 입력에 대해서 출력을 구해 봅니다.

웨이트2 바이어스1로 고정되어 있는 상황에서 다양한 입력에 따라 서로 다른 출력 값이 나오는 것을 알 수 있습니다.
다른 답을 원한다면?
만약 출력이 나왔는데 이것이 원하는 답이 아니라면 어떻게 할 것인가?

입력 1에 대해서 3이 나왔는데 우리가 원하는 것은 입력 1에 대해서 4라면 어떻게 할 것인지에 대해서 다뤄봅시다. 입력 x가 웨이트 2와 바이어스 1을 만나서 어파인 썸을 하고 액티베이션 펑션을 거쳐서 출력이됩니다. 입력이 고정되어 있고 액티베이션 펑션은 뉴럴의 특성이기 때문에 수정을 할 수 없다면 우리가 고칠 수 있는 것은 w와 b값 밖에 없습니다. 뉴럴이 어떤 성질 즉 어떤 답을 낼지를 결정하는 것은 w값과 b값이 되는 것입니다. 우리는 w값과 b값을 조절해서 원하는 값을 만들어야 합니다.
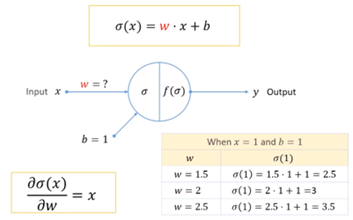
웨이트w를 업데이트를 해보겠습니다. 처음에 임의로 결정한 웨이트 값이 2였습니다. 그래서 이것을 1.5로도 바꿔보고 2.5로도 바꿔봅니다.

1.5에서는 2.5를 출력하였고 2.5에서는 3.5를 출력하는 것을 확인 할 수 있습니다.
시그마 함수를 w에 대해서 미분을 하게 되면 x가 나옵니다.
(편미분 기호지만 이는 추후 설명)

여기에서 우리는 이것이 어떠한 의미를 갖는지만 이해하면 충분합니다. 만약 x에 영을 넣으면 양수가 나옵니다. 이것의 의미는 w값이 증가하면 시그마도 증가한다는 의미입니다. 막약 x가 음수였다면 w값이 증가하면 시그마 값은 감소한다는 의미입니다.
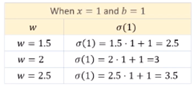
여기서는 w값이 증가하면 시그마 값도 증가하는 경향성을 갖고 있습니다.
같은 방법으로 바이어스도 업데이트를 해보겠습니다.
임의로 결정한 바이어스 값이 1이였습니다.

바이어스 값을 줄여보기도 하고 늘여보기도 해보니 시그마 값도 줄어 들고 늘어납니다.

시그마를 b에 대해서 미분을 하게 되면 1이 나옵니다. 마찬가지로 양수입니다. b를 증가 시키면 시그마도 같이 증가 한다는 의미겠죠. 반대로 시그마를 증가 시키고 싶으면 b를 증가시켜야 한다는 의미도 됩니다.

Identity 함수를 사용하고 있으므로 f(σ)의 값이 시그마(σ)입니다. 시그마 값을 2.5, 3, 3.5를 넣으면 f(σ)값도 2.5, 3, 3.5가 나옵니다. 출력 값이 증가하려면 시그마 값이 증가해야 합니다. 이전에 보았던 것과 같이 시그마 값이 증가하려면 w값 혹은 b값이 증가 해야한다는 일련의 과정을 관찰 할 수 있습니다.

지금까지 얘기를 정리한 것입니다. 우리가 지금 원하는 것은 현재 y값이 3이 나왔는데 4가 나왔으면 좋겠다 입니다.

w가 증가하면 시그마가 증가하고, 시그마가 증가하면 f도 증가합니다. f와 y는 같기 때문에 결과적으로 w가 증가하면 y값을 증가시킵니다. 이런 것을 체인 룰이라고 부릅니다. 마치 분자분모처럼 돼서 소거해서 지우는 것처럼 생각해도 이해하기 편합니다.

b에 대해서도 동일하게 b가 증가하면 시그마가 증가하고, 시그마가 증가하면 f도 증가합니다. f와 y는 같기 때문에 b가 증가하면 y가 증가합니다.
w값과 b값을 이렇게 저렇게 넣어 보다보면 원하는 y값이 나오는 조합을 찾을 수도 있겠죠 하지만 우리가 실제로 만들고자 하는 것은 뉴럴네트워크의 굉장히 복합한 형태입니다. 그러니까 w와 b를 어떻게 시도를 해 가면서 찾을 수 있는 구조가 아닙니다.
Back-propagation(역전파)
그래서 나온 방식이 역전파 하는 방식입니다. Back-propagation 알고리즘은 어떤 오류를 반대 방향으로 전파시키는 것입니다.

우리가 원하는 값을 ytarget이라고 하고 현재 나온 값이 y라고 하면 이 차이값을 이용해서 오차가 어느 정도라는 것을 얘기를 할 수가 있습니다. 타겟 값과의 차이의 제곱에 1/2을 곱하는 것을 오류 펑션으로 정의합니다.
오류 펑션이 거꾸로 거슬러 올라가면서 우리가 원하는 w와 b값을 찾아주는 것처럼 사용하는 방식입니다.
지금은 뉴런이 하나빡에 없기 때문에 거꾸로 거슬러 간다는 느낌이 그렇게 강하지 않은데 나중에 뉴런의 개수가 많아지고 이 층이 많아지게 되면 그 때는 역전파라는 느낌이 훨씬 강하게 느껴집니다.
Gradient Descendent Method
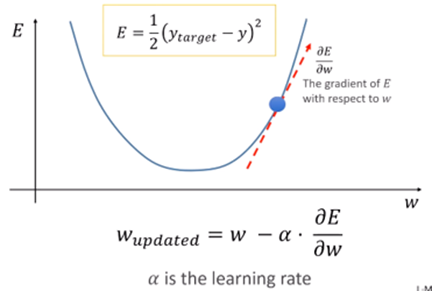
우리는 미분을 이용해서 w값이 어떻게 변했을 때 E값이 줄어드는가를 알수가 있습니다. 만약에 우리가 w값을 변화 시켰을때 E값이 증가 할 것인지 감소 할 것인지 알 수 있다면 우리는 이 w값을 찾아 갈 수 있지 않을까라는 것이 Gradiant Descendent Method의 핵심입니다.
e 값을 w로 미분을 하면 곡선의 기울기 값이 나옵니다. 그러면 우리는 w를 증가하는 방향으로 e값이 가파르게 증가하는구나 그래서 우리는 e값을 감소시키기 위해서는 거꾸로 가야 겠구나.

w에 대한 그레디언트 e의 반대방향으로 가야 겠구나하는 것이 하강하는 그레디언트의 반대방향으로 가겠다는 기법입니다. 그래서 식에서 마이너스인것입니다.
식을 다시보면 E값을 조금 더 줄여주는 w값을 찾고 싶다면 현재의 w값에서 E경사의 반대방향이기 때문에 마이너스가 붙었고 학습 계수인 알파값(α)이 붙었습니다. 이 α값이 작으면 느리게 가고 α값이 너무 크면 이상한 곳으로 가버립니다. 알파 값을 너무 작게하면 느려기고 너무 크게 하면 불안정하게 됩니다. 적절한 값을 찾는 것이 중요한 노하우가 됩니다.
Train을 통한 더 나은 w 구하기
Gradient descendent를 이용해서 w값을 좀 더 나은 값으로 바꿔주는 내용을 살펴보겠습니다.

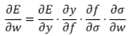
w값을 바뀌어 e값이 어떻게 변하는지를 알아보기 위해서 연쇄적인 개념을 사용합니다. 식이 복잡해 보이지만 조금 들어다 보면 단순하고 재미있습니다. w가 바뀌었을 때 시그마가 어떻게 바뀌느냐, 그 다음 것은 시그마를 바뀌었을 f가 어떻게 바뀌느냐, f를 바꾸었을 때 y가 어떻게 바뀌느냐, 마지막으로 y를 바꾸었을 때 E가 어떻게 바뀌느냐입니다. 분자 분모 소거하듯이 소거 소거를 하고 나면 라운드 E 라운드 w이기 때문에 결국 좌변과 우변이 같습니다. 연쇄작용을 이용해서 w가 바뀌었을 때 E가 어떻게 바뀌는 것을 찾는 것입니다. w값이 변했을 때 e값이 증가하는지 감소하는지 알면 E값이 줄어드는 방향을 찾아 들어 갈 수 있는 것입니다.

앞에서 봤듯이 ∂σ/∂w는 x였죠. 액티베이션 펑션으로 Identity를 사용할 경우 ∂f/∂σ는 1입니다. ∂y/∂f는 둘이 동일하므로 1이 되는 거죠. ∂E/∂y의 미분은 y-ytarget입니다. y와 ytarget은 각각 3과 4이므로 -1입니다. 입력 x는 1이고므로 결국 ∂E/∂w = -1⋅1⋅1⋅1 = -1 입니다.

Y - Ytarget = -1 의미는
미분의 결과가 음수이니까 반대 방향 y값이 커질수록 에러는 줄어 든다는 뜻입니다. 현재 y가 3이고 y값이 4가 바라는 값입니다. y값이 4와 가까워 질때까지 y값이 증가하면 에러가 줄어 드는 것을 알 수 있습니다.

러닝 레이트 알파(α)를 0.1로 넣고 계산을 해보면 wupdated값이 2.1이 나옵니다. 즉, [Train]을 통해 더 나은 w값으로 2.1을 구했습니다.
Train을 통한 더 나은 b 구하기
이제 바이어스b에 대해서도 같은 과정을 적용해봅시다. b값을 더 나은 값으로 업데이트 하는 과정입니다.
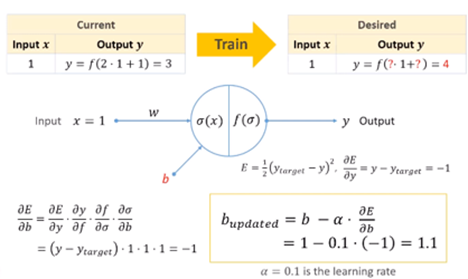
웨이트w에서와 마찬가지로 체인룰을 적용해 봅니다. 이 과정은 b가 변하면 시그마σ가 어떻게 변하고, σ가 변하면 f가 어떻게 변하고, f가 변하면 y가 어떻게 변하고, y가 변하면 E가 어떻게 변하는지를 식으로 보여주고 있습니다. 이는 결국 소거하여 b가 변하면 E가 어떻게 변하는지와 같습니다.
앞에서 봤듯이 ∂σ/∂b는 1이 였습니다. 액티베이션 펑션이 identity를 사용하고 있으며 만약 다른 액티베이션 펑션이면 해당하는 그 펑션을 미순해서 계산하면 됩니다. 여기서는 앞에와 같은 방식으로 미분하여 ∂E/∂b = -1⋅1⋅1⋅1 = -1을 얻을 수 있습니다. 이것이 의미하는 것은 음수이므로 b가 증가 할 때 E값은 감소한다는 것을 의미합니다.

이를 반영해서 에러를 줄여주는 b값을 찾을 수 있습니다. [Train]을 통해 더 나은 b값으로 1.1을 구했습니다.
Back-propagation(역전파)로 훈련
실제로 계산한 결과를 보겠습니다.

충분히 작은 E값을 얻을 때까지 Feed-forward를 해보고 Back-propagation을 하여 w와 b값을 업데이트합니다.
트레인을 거듭하면서 w, b값을 업데이트하다가 66번째 Train에서 결국 y값 4가 나온다는 것을 훈련하는 하는 것을 볼 수 있습니다.
인공 지능에서의 미분의 활용
자주 사용되는 Activation function

프로그래밍에서 미분을 구할 때는 크게 두 가지 방식으로 구분합니다.
Analytical differentiation: 수학자들이 유도해둔 공식을 외우듯이 해서 사용하는 방식을 표를 찾아서 사용하는 방식입니다.

Numerical differentiation: Δx값이 작으면 작을 수록 실제 도함수와 같아지겠죠. 그렇지만 컴퓨터는 무한소를 다룰 수 없기에 유한하지만 작은 숫자를 사용해서 적당시 근사 할 수 있습니다. 해석적인 미분방식과 달리 그냥 값을 넣어버립니다. 어떤 함수가 있다면 어떤 값을 넣고 구한 값과 그 값으로 부터 적당히 작은 수치 만큼 변한 값을 넣고 구한 값의 차이를 다시 Δx로 나누어 주면 우리가 수치미분 값을 얻을 수 있는 것입니다.
수치 미분의 예시)
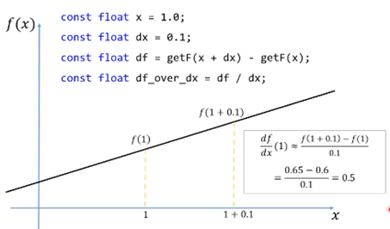
미분의 활용1)
변화한 값을 직접 함수를 실행하지 않더라도 그 추청할 수 있다.

x가 1의 지점에서 f(1)은 0.6이고 이 지점에서의 df/dx(1)은 0.5이다. 즉, 특정 지점에서의 함수값과 미분값을 알고 있다면 1에서 0.2만큼 더 나아갔거나 혹은 x는 1 근처의 값들을 함수 f를 직접 계산하지 않고 추측을 할 수 있습니다.

처음식에서 Δx를 좌변으로 옮겨줍니다. -f(x)를 다시 좌변으로 옮겨줍니다. 좌변 우변을 바꿔주고 Δx에다가 Δxtarget을 넣어 준다면 최종식이 됩니다.
함수 f에 x + Δxtarget 값을 직접 넣지 않아도 정확한 값이 아니라 비슷한 값을 알겠다는 의미입니다. 앞에서 가정 했던 것과 같이 함수값(f(x))와 미분값(df/dx(x))는 이미 알고 있습니다.

이러한 방식으로 정확한 값이 아니더라도 추정을 하는 것을 Extrapolation이라고 합니다. Δxtarget가 0.2인 경우를 추정해 보았습니다.
미분의 활용2)
원하는 아웃풋을 얻기 위해서는 어떤 인풋을 넣어야 하는지가 궁금할 때가 있습니다. 예를 들어 0.7을 얻기위해서는 어떠한 인풋을 넣어야 하는지 궁금할 때가 있습니다.

x에 대한 모든 값을 구해서 알아 내는 방법도 있겠지만, 한 점에 대해서 값을 내어보고 그 지점으로 부터 얼마를 바꾸면 원하는 값을 내줄 것이냐로 접근할 수 있습니다.
예를들어 아이가 1시간을 공부 했더니 10점을 받아 왔고 30분을 공부를 더 했더니 20점을 받아 왔습니다. 그럼 이 아이가 몇 시간을 더 공부해야 100점을 받아 오는지를 추론하고 싶을때가 있겠죠 이 때 사용하는 것과 동일한 개념입니다.
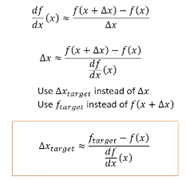
예시입니다)

원하는 값이 0.8이고 f(1)의 값은 이미 알고 있는 값으로 0.6이고 df/dx(1)값을 구해서 0.5가 나오고 계산해 보면 0.2가 나옵니다. 그래서 x = 1 + 0.2를 넣어 보면 0.7이다라고 추측이 가능한 것입니다.
'AI' 카테고리의 다른 글
| SpecKit, 스펙 기반 개발 툴킷 (0) | 2025.09.11 |
|---|---|
| 딥러닝 첫걸음 (5) | 2025.08.26 |