데브 지노 - 지노윈의 개발 스토리

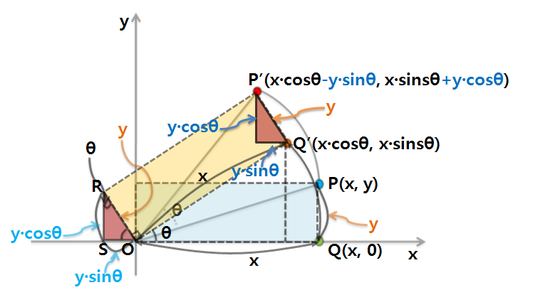
내적\(\mathbf{A\cdot B=\left|A\right|\left|B\right|\cos\theta}\) 벡터의 내적은 같은 차원의 두 벡터가 주어졌을 때, 벡터를 구성하는 각 성분을 곱한 후 이들을 더해 스칼라를 만들어내는연산입니다. 즉, 두 벡터가 결국 스칼라로 됩니다. 게임에서는 물체를 랜더링 할 때 밝은 곳과 어두운 곳이 생기는데 이것을 계산 할 때 내적이 사용됩니다. 보이지 않는 곳을 제외 할 때도 사용합니다. 전투 판정에서도 앞뒤 판정이나 타겟이 얼마의 각도에 있는지를 알고자 할 때 사용합니다. 앞뒤 판별\(\mathbf{A\cdot B > 0}\) : 두 벡터의 내적의 결과가 0보다 크면 두 벡터가 이루는 각이 예각이므로 캐릭터 앞에 목표물이 있다고 판별 할 수 있습니다.\(\math..

미분은 영어로 differential(차이) 이고, 한자로는 잘게 나누다는 뜻입니다. 미분 이해의 열쇠는 평균 변화율입니다. 그리고 또하나의 열쇠는 극한입니다. 극한을 이해하지 않고 미분·적분을 제대로 이해 할 수 없습니다. 극한을 이해 하는 이해하는 것은 \(\infty\)(무한대)를 이해하는 것입니다. 미분은 문자 그대로 '미세하게 나눈다'는 말입니다. 즉, 미분은 함수를 한없이 작게 나누는 분석입니다. 무한대는 문자 그대로 '끝없이 크다'는 말인데 이를 상상하기 가장 쉬운 것이 바로 '등차 수열'과 '등비 수열'입니다. 다음의 등차 수열 관련 정의가 낯설다면 다음 글을 참고하세요. : [게임 개발/게임 수학] - 등차 수열 [등차 수열의 일반항] \(\mathbf{a_n} = \mathbf{a_1}..

순열 순열(Permutation)은 객체를 순서에 따라 배열하는 방법의 수를 나타내는 것입니다. 즉, 순서를 고려하여 뽑는 경우의 수. A, B, C, D, E 5개의 문자중에서 순서를 고려하여 3개를 뽑는 경우의 수는 60(5x4x3)가지입니다. 처음에는 5개 중에서, 다음은 4개 중에서, 그 다음은 3개 중에서 뽑을 수 있기 때문입니다. 기호로 표시하면 다음과 같습니다. $${_5}P{_3}=5\times4\times3 = 60$$ 조합 조합(Combination)은 n개의 객체 중에서 r개의 객체를 선택하는 방법의 수를 나타내는 것입니다. 즉, 선서를 고려하지 뽑는 경우의 수. A, B, C, D, E 5개의 문자중에서 순서를 고려하지 않고 3개를 뽑는 경우의 수는 10가지 입니다. 순서를 고려 했..

\(\mathbf{a_1}\) \(\scriptstyle\text{*r}\to\) \(\mathbf{a_2}\) \(\scriptstyle\text{*r}\to\) \(\mathbf{a_3}\) \(\scriptstyle\text{*r}\to\) \(\mathbf{a_4}\) 일정한 수를 곱한 수열을 '등비 수열'이라 합니다. \(\mathbf{a_4} = \mathbf{a_1}r^3\) 등비 수열의 4번째 항 \(\mathbf{a_4}\)는 \(\mathbf{a_1}\)에 r을 3번 곱한 값입니다. r을 공비라 합니다. [등비 수열의 일반항] \(\mathbf{a_n} = \mathbf{a_1}r^{n-1}\) 등비 수열의 합을 알아 봅시다. [등비 수열의 합] \(\mathbf{S_n} = {{\ma..

\(\mathbf{a_1}\) \(\scriptstyle\text{+d}\to\) \(\mathbf{a_2}\) \(\scriptstyle\text{+d}\to\) \(\mathbf{a_3}\) \(\scriptstyle\text{+d}\to\) \(\mathbf{a_4}\) 앞의 수와 일정한 차이가 있는 수열을 '등차 수열'이라 합니다. \(\mathbf{a_4} = \mathbf{a_1} +3d\) 등차 수열의 4번째 항 \(\mathbf{a_4}\)는 \(\mathbf{a_1}\)에 d를 4번 더한 값입니다. \(\mathbf{a_1}\)을 초항, d를 공차라 합니다. [등차 수열의 일반항] \(\mathbf{a_n} = \mathbf{a_1} + (n - 1)d\) 등차 수열의 합은 다음과 같이 ..

\(Q \to Q', P \to P'\)로 회전하는 모습입니다. \(Q(x, 0)\)는 \(Q'(x\cdot\cos\theta, x\cdot\sin\theta)\) \(P'는 Q'에서 (-y\cdot\sin\theta, y\cdot\cos\theta)\)를 한것과 같습니다. \(x' = x\cos\theta - y\sin\theta\) \(y' = x\sin\theta + y\cos\theta\) 다음과 같이 증명을 할 수 있습니다. https://color-change.tistory.com/54 (기하와 벡터) 회전변환 식 유도 ::(기하와 벡터) 회전변환 식 유도:: - 개념, 공식, 증명, 유도 이 포스팅은 기하와 벡터의 회전변환 공식을 유도하는 글 입니다. 회전변환은 고교 수학(자연계) 기하와 벡..

각도법(Degree) 0~360까지의 수를 사용하여 각의 크기를 잰다. \(1 rad \approx 57.2958^\circ...\) 호도법(Radian) 호의 길이를 기준으로 각을 측정하는는 방법이다. 즉, 호의 길이가 1이 되는 부채꼴의 각을 기준으로 각을 측정한다. 원의 둘레는 지름의 대략 3.14배이다. 이것이 바로 3.141592... 무리수인 원주율 파이(\(pi\))이다. \(1 radian\) https://ko.wikipedia.org/wiki/%EC%9B%90%EC%A3%BC%EC%9C%A8 원주율 - 위키백과, 우리 모두의 백과사전 위키백과, 우리 모두의 백과사전. 3.1415926535897932384626433832795…… 원주율(圓周率, 문화어: 원주률)은 원둘레와 지름의 비 ..

야코프 베르누이(독일어: Jakob Bernoulli, 1654년 12월 27일 ~ 1705년 8월 16일)는 스위스의 수학자이자 화학자이다. 극좌표계(Polar coodinate system) ㅇ 평면 상의 위치를 `거리`와 `각도`로써 지정하는 방법 - 스위스 수학자, 야코프 베르누이(Jakob Bernoulli, 1654~1705)에 의해 고안되었다 함 극점(원점)으로부터 `유향 거리(r)`와 `유향 방향(θ)`으로 정하는 2차원 평면 좌표계 - O : 원점(origin) 보다는 극점(pole) 이라는 용어를 더 많이 씀 - r : 극점 O로부터 점 P까지의 유향 거리(directed distance) - θ : 시계반대방향의 유향 각도(directed angle) - P(r,θ) : 극좌표 점 표..

나는 생각한다, 고로 존재한다. 데카르트 좌표계 직선의 수 집합을 수직으로 배치해 평면을 표기하는 방식입니다. 우리가 흔히 볼 수 있는 좌표계로 데카르트 좌표계가 있다. 철학자이자 수학자인 르네 데카르트가 천장을 날아다니며 옮겨붙는 파리를 통해 영감을 얻고 해당 좌표계를 발명했기에 데카르트의 이름이 붙어 있다. 2차원용의 데카르트 좌표계는 다음과 같다. 오른쪽 위부터 반시계 방향으로 제1사분면, 제2사분면, 제3사분면, 제4사분면이라고 한다. 데카르트 좌표계라고 하면 고등학교 때까지 배운 2·3차원 직각 좌표계를 뜻한다. 과학에서 쓰일 때 보통 X축이 독립변인, Y축이 종속변인을 나타낸다. 도수분포를 나타낼 때에는 X축이 계급구간을, Y축이 도수를 나타낸다. https://namu.wiki/w/%EC%A..

함수 \({\displaystyle f}\)와 그 역함수 \({\displaystyle f^{-1}}\) 역함수(Inverse function)? 정의역과 치역을 서로 뒤바꾸어 얻는 함수이다. 즉, 역함수의 대응 규칙에서, 원래의 출력값은 원래의 입력값에 대응한다. 성질 역함수를 가질 필요 충분 조건은 전단사 함수이다. \({\displaystyle (f^{-1})^{-1}=f}\) \({\displaystyle f^{-1}(f(x))=x\qquad (\forall x\in X)}\) \({\displaystyle f(f^{-1}(y))=y\qquad (\forall y\in Y)}\) \({\displaystyle f^{-1}\circ f=\operatorname {id} _{\operatorname ..