반응형

\(Q \to Q', P \to P'\)로 회전하는 모습입니다.
\(Q(x, 0)\)는 \(Q'(x\cdot\cos\theta, x\cdot\sin\theta)\)
\(P'는 Q'에서 (-y\cdot\sin\theta, y\cdot\cos\theta)\)를 한것과 같습니다.
\(x' = x\cos\theta - y\sin\theta\)
\(y' = x\sin\theta + y\cos\theta\)
다음과 같이 증명을 할 수 있습니다.

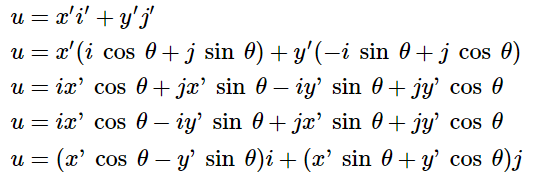
https://color-change.tistory.com/54
(기하와 벡터) 회전변환 식 유도
::(기하와 벡터) 회전변환 식 유도:: - 개념, 공식, 증명, 유도 이 포스팅은 기하와 벡터의 회전변환 공식을 유도하는 글 입니다. 회전변환은 고교 수학(자연계) 기하와 벡터 과목의 전반부에서 처
color-change.tistory.com
반응형
'게임 개발 > 게임 수학' 카테고리의 다른 글
| [수학] 등비 수열 (0) | 2023.03.22 |
|---|---|
| [수학] 등차 수열 (0) | 2023.03.19 |
| 각도법 & 호도법 (0) | 2022.12.18 |
| 극좌표계(Polar coodinate system) (0) | 2022.12.13 |
| 데카르트 좌표계 (2) | 2022.12.11 |