[수학] 등비 수열

 

 

${\mathbf{a}}_{\mathbf{1}}$ $\text{*r}\to$ ${\mathbf{a}}_{\mathbf{2}}$ $\text{*r}\to$ ${\mathbf{a}}_{\mathbf{3}}$ $\text{*r}\to$  ${\mathbf{a}}_{\mathbf{4}}$

일정한 수를 곱한 수열을 '등비 수열'이라 합니다.

 

${\mathbf{a}}_{\mathbf{4}}={\mathbf{a}}_{\mathbf{1}}{r}^3$

등비 수열의 4번째 항  ${\mathbf{a}}_{\mathbf{4}}$는  ${\mathbf{a}}_{\mathbf{1}}$에 r을 3번 곱한 값입니다.

r을 공비라 합니다.

[등비 수열의 일반항]
${\mathbf{a}}_{\mathbf{n}}={\mathbf{a}}_{\mathbf{1}}{r}^{n-1}$ 

 

등비 수열의 합을 알아 봅시다.

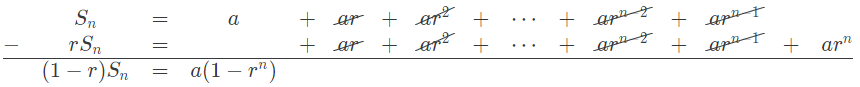
[등비 수열의 합]
${\mathbf{S}}_{\mathbf{n}}=\frac{{\mathbf{a}}_{\mathbf{1}}(1-r^n)}{1-r}$ (단, $r\ne 1$)